Lossless data compression

By

Lossless data compression is the art of making files smaller, by applying various clever techniques designed to take advantage of the patterns in a file in order to create a compressed version that uses less space, but can be decompressed to form the original file.

I was fascinated by lossless compression for quite a long time, but didn't had the chance to study it in depth, until I've recently found the excellent Data Compression lectures of Bill Bird on YouTube about DEFLATE, Bzip2, Arithmetic Coding and several other methods.

# Basic techniques

In this section we will present various basic techniques used in data compression.

## Elias gamma coding

Given a list of non-negative integers, this method will encode them as a sequence of bits. [ref]

For example, let `n = 13`, which in binary is `1101`. We strip the most significant bit and consider only `101`.

Then we encode the length of this truncated binary representation, using unary coding (a run of `1` bits), where the number of ones represent the length of the truncated binary representation (length of `101` in our case).

We terminate the unary coding with bit `0` followed by the actual bits of the truncated binary representation of the run-length.


In our case, for `n = 13`, we emit the following bits:

    1111 0 101

When decoding the data, we read bits until we encounter the first bit `0`. Then we read as many bits as `1` bits we've encountered. We prepend the `1` bit to those bits and convert them into a number.

Alternatively, we can omit one bit from the unary encoding, using the following encoding:

  • encoding `n = 0` as: 0
  • encoding `n = 1` as: 1 0 0
  • encoding `n = 2` as: 1 0 1
  • encoding `n = 3` as: 11 0 00


In general, for `n >= 1`, we increment `n` by one, ensuring that it has at least `2` bits, encoding `n = 13` as:

    111 0 110

## Double Elias gamma coding

When encoding very large integers, the unary part of Elias gamma coding will become pretty long, but we can do better!

Let `n = 7787064`, which in binary is 11101101101001000111000.

Using Elias gamma coding, we would encode `n` as:

    1111111111111111111111 0 1101101101001000111000

In double Elias gamma coding, we encode the length of the unary part using Elias coding as well:

            my $t = sprintf('%b', $n + 1);
            my $l = length($t);
            my $L = sprintf('%b', $l);
            my $bitstring = join('', '1' x (length($L) - 1), '0', substr($L, 1), substr($t, 1));

Which encodes `n` as:

    1111 0 0111 1101101101001000111001

## Delta coding

Delta coding is a technique for encoding a list of integers that are relatively close to each other (i.e.: the difference between consecutive terms is small).

For example, if we have:

    L = [10, 11, 12, 11, 13, 13]

We start by computing the differences of consecutive terms:

    D = [10, 1, 1, -1, 2, 0]

Then we can encode the differences as:

  • `0` is encoded with bit `0`
  • a positive value is encoded with leading `10` bits followed by its Elias gamma coding
  • a negative values is encoded with leading `11` bits followed by its Elias gamma coding


In our case, `D` is encoded as:

    101110010 100 100 110 10100 0

## Fixed-width binary coding

When encoding a list of non-negative integers that are in increasing order, but not necessarily close to each other, we can do slightly better than Elias coding and Delta coding, by simply encoding them with fixed-width bits, increasing the width as the numbers grow.

For example:

    L = [3, 5, 9, 10, 30, 50, 55]

Is encoded in the following sequence of bits:

    11 101 1001 1010 11110 110010 110111

However, in order for being able to decode them, we need to generate a header, telling us how many integers are of a fixed-width:

    [[2, 1], [3, 1], [4, 2], [5, 1], [6, 2]]

We can encode the header using Elias coding or Delta coding.

## Run-length encoding (RLE)

Run-length encoding compresses runs of symbols, by giving the initial symbol, followed by its run-length decremented by `1`:

    "aaaaaaaaaaaaabbbbbbbbbbbbbbccccccccccdddefgggg" --> "a[12]b[13]c[9]d[2]e[0]f[0]g[3]"


Another approach (used in Bzip2), is to emit a run-length only when we've seen `4` consecutive identical symbols. In this case, the run-length is decremented by `4`:

    "aaaaaaaaaaaaabbbbbbbbbbbbbbccccccccccdddefgggg" --> "aaaa[9]bbbb[10]cccc[6]dddefgggg[0]"

This is beneficial for inputs that do not include many runs of consecutive identical characters.

The values in brackets are encoded as bytes and therefore the maximum run-length is limited to `255`.

## Variable run-length encoding (VRLE)

This is another variant of run-length encoding, in which we encode the run-lengths using Elias coding.

    "aaaaaaaaaaaaabbbbbbbbbbbbbbccccccccccdddefgggg"

is encoded as:

    01100001 1110101 01100010 1110110 01100011 1110010 01100100 101 01100101 0 01100110 0 01100111 11000

## Binary run-length encoding

Variable run-length encoding can also be applied to a sequence of bits: 

    101000010000000010000000100000000001001100010000000000000010010100000000000000001

which is encoded as:

    1000110101110110111010011110001010101100011110101010000111101110

The idea is the same as above, but instead of operating on 8-bit chunks, we operate on individual bits.

## Huffman coding

Huffman coding is an entropy coding method, which represents commonly occurring characters using fewer bits.

By applying Huffman coding on the following string (`312` bits):

    "this is an example for huffman encoding"

which is equivalent with the following sequence of bytes:

    [116, 104, 105, 115, 32, 105, 115, 32, 97, 110, 32, 101, 120, 97, 109, 112, 108, 101, 32, 102, 111, 114, 32, 104, 117, 102, 102, 109, 97, 110, 32, 101, 110, 99, 111, 100, 105, 110, 103]

we get the following dictionary:

110: 000
109: 0010
111: 0011
115: 0100
100: 01010
103: 01011
108: 01100
112: 01101
114: 01110
116: 01111
117: 10000
120: 10001
101: 1001
 32: 101
102: 1100
105: 1101
 97: 1110
 99: 11110
104: 11111

Allowing us to encode it in only `157` bits:

01111 11111 1101 0100 101 1101 0100 101 1110 000 101 1001 10001 1110 0010 01101 01100 1001 101 1100 0011 01110 101 11111 10000 1100 1100 0010 1110 000 101 1001 000 11110 0011 01010 1101 000 01011

However, we also need the above dictionary in order for being able to decode the bits.

When the symbols are sorted in lexicographical order, we only need to transmit the frequency of each symbol in order reconstruct the dictionary. Additionally, we only need to transmit the frequencies of characters in a given range, from the smallest symbol to the largest symbol in our table.

In our case, the smallest symbol is `32`, while the largest is `120`, so we have the following sequence, representing the frequency of each symbol in our range:

6 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 3 0 1 1 3 3 1 2 3 0 0 1 2 4 2 1 0 1 2 1 1 0 0 1

Using Run-length encoding + Elias coding, we can encode the above sequence in `13` bytes as:

11101000111111000000011010001010011011001001100011010010010011000111000011000100001001100010100010010000

## Move-to-front transform (MTF)

The move-to-front transform is a clever technique which replaces each symbol by its index in a stack of recently seen symbols.

The transform is useful for replacing a long run of identical symbols with a run of zeros.

See also:


## Burrows-Wheeler transform (BWT)

The Burrows-Wheeler transform is a block-sorting method that rearranges a string into runs of identical characters.

 While it's quite easy to implement the BWT algorithm, some cleverness is needed in order to make the implementation practical for large inputs. 

I will not go into details here, but please do watch the following videos if you're interested to learn more about it:


# Bzip2

The Bzip2 method is just a pipeline of RLE + BWT + MTF + ZRLE + entropy coding.

The RLE is the `8`-bit RLE, which emits a run-length only for 4 or more consecutive identical bytes.

This step was added in order to fix some performance issues with the Burrows-Wheeler transform on inputs with long runs of identical characters.

After applying the Burrows-Wheeler transform (BWT) on the output of RLE, we then apply the Move-to-front transform on the BWT, which replaces runs of identical characters with zeros.

The ZRLE replaces runs of zeros with the digits of the binary representation of the run-length and increments each other symbol by one, such that symbol `1` becomes `2`, symbol `2` becomes `3`, etc.

The resulting symbols are then encoded with an entropy-coding method (usually, Huffman coding or Arithmetic coding).

Basic implementations:

These `5` simple steps are enough to outperform the DEFLATE method on text files, which is arguably more complex than Bzip2.


# LZ77 method

The LZ77 method, named after its inventors, Lempel and Ziv, compresses data by replacing previously seen sub-strings with back-references.

For example, the string "TOBEORNOTTOBEORTOBEORNOT" is compressed as:

    [0,0]T[0,0]O[0,0]B[0,0]E[1,1]R[0,0]N[1,1]T[0,6]T[1,7]T

Where the values in brackets represent the index and the length of the sub-string to be substituted in when decompressing:

    [0, 0, "T"] -> T
    [0, 0, "O"] -> TO
    [0, 0, "B"] -> TOB
    [0, 0, "E"] -> TOBE
    [1, 1, "R"] -> TOBEOR
    [0, 0, "N"] -> TOBEORN
    [1, 1, "T"] -> TOBEORNOT
    [0, 6, "T"] -> TOBEORNOTTOBEORT
    [1, 7, "T"] -> TOBEORNOTTOBEORTOBEORNOT

The encoding of indices and lengths require some cleverness. For practical reasons, lengths are limited to `255`, which allows us to encode them as bytes. Preferably, encoding them using Huffman coding.

However, indices are generally much larger and require a different approach.

One simple solution would be using fixed-width binary coding:


A more advanced solution would be using offset bits:


An improved variant of LZ77 is LZSS, which emits a back-reference only when it's beneficial (i.e.: does not inflate the data):


This variant also encodes the indices and the lengths using offset bits, which achieves better compression in general.


# Beyond bzip2

When it was developed by Julian Seward, back in 1996, bzip2 provided much better compression-ratio than DEFLATE on almost all inputs (especially on text files) and it was state-of-the-art for several years. However, since then, some more progress was made on data compression.

Currently, the state-of-the-art general-purpose method when it comes to compression-ratio, is the ZPAQ method (with the -m5 option), beating bzip2, bzip3 and 7-zip across the board. However, despite providing the best compression-ratio, it is quite slow to use in practice, especially when compressing big files. Another downside of ZPAQ is that decompression is also slow. It does have some uses in compressing small files when the size really matters (e.g.: when transmitting data over a slow connection).

The second best general-purpose compression method, in terms of compression-ratio, is LZMA (implemented in the .xz, .lz, .7z and .lzma formats). The compression step is also quite slow (however, faster than ZPAQ), but the decompression is pretty fast.

Surprisingly, a basic combination of LZ77 + BWT ("lzbw") (source code) outperforms most modern compressors, including 7-zip, on some input files:


The "a.txt" file can be generated with Sidef, using the following command:

    sidef -E 'print squarefree(164498).join(" ")' > a.txt

While the "lzbw" method beats 7-zip on this particular file, it does not outperforms it in general.

Yet another basic combination of BWT + Variable RLE (source code) is particularly good at compressing files with long runs of consecutive identical characters (e.g.: PPM images).

# Compression methods comparison

The input file, "all.tar", contains 3 files:



The following image shows a comparison of compression methods, sorted by the size of the resulted compressed file:

The top compression methods being ZPAQ, Bzip3, BSC, followed by Lzip, xz and 7-zip.

It seems that the Burrows-Wheeler transform is making a comeback, as both Bzip3 and BSC are powered by it.

# Implementations

Below we have source-code implementations of the presented compression techniques in Sidef and Perl programming languages:

Sidef:

Perl:

Update (21 March 2024): this post led to the creation of a new Perl module, called Compression::Util, which implements various techniques used in data compression and can be used to quickly put together new compression methods:

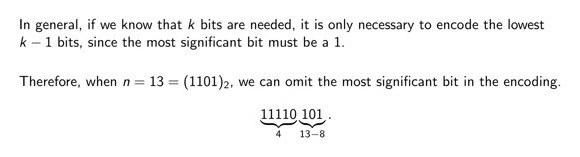
Comments

Post a Comment