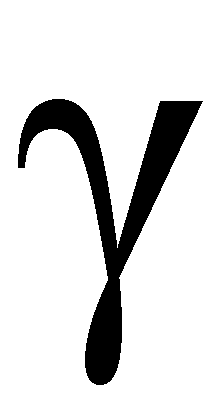Mathematics and computer science

In 2001,  Jeffrey Lagarias  proved that the  Riemann hypothesis  is equivalent to the following statement ( proof here ): `\sigma(n) <= \H_n + \ln(\H_n)*\exp(\H_n)` with strict inequality for `n > 1`, where `\sigma(n)` is the sum of the positive divisors of `n`. In 1913,  Grönwall  showed that the asymptotic growth rate of the  sigma function  can be expressed by: `\lim_{n to \infty}\frac{\sigma(n)}{\n \ln\ln n} = \exp(\gamma)` where  lim  is the  limit superior . Relying on this two theorems, we can show that: `lim_{n to \infty}\frac{\exp(\gamma) * n \ln \ln n}{\H_n + \ln(\H_n) * \exp(\H_n)} = 1` with strict inequality for each `1 < n < \infty` (see  Wolfram|Alpha ): `\exp(\gamma) * n \ln \ln n < \H_n + \ln(\H_n) * \exp(\H_n)` If the Riemann hypothesis is true, then for each `n ≥ 5041`: `\sigma(n) <= \exp(\gamma) * n \ln \ln n` By using the usual definition of the `\gamma` constant: `\gamma = \lim_{n to \infty}(\H_n - \ln n)`

In this post we're going to take a look at a mysterious mathematical constant, called the Euler–Mascheroni constant , and its fascinating role in harmonic and prime numbers. # Is `gamma` transcendental? This constant, although it has a fairly simple definition, it is currently not known whether it is rational or irrational, but it is widely believed by mathematicians to be  transcendental , which also implies that it is irrational. It is usually defined as:  `\gamma = \lim_{n to \infty}(\H_n - \ln n)` where `\H_n` is the `n` th   harmonic number , which is defined as: `\H_n = \sum_{k=1}^(n)\frac{1}{k}` # "Proving" that `\gamma` is transcendental There exists a  proof that `\gamma` is transcendental, but the proof is very subtle: By Lindemann–Weierstrass theorem , the natural logarithm of any positive algebraic number other than 1 is a transcendental number . The `n` th  harmonic number is rational. As all rational numb

In this short post we're going to take a look at why `0/0` is really undefined. # Overview It's an old mathematical issue, which has been debated many times over the centuries with mostly the same result: `0/0` does not have a defined value. But now, we're going to take a look at why this is true. # Illustration To illustrate this, let's consider the following sum: `\sum_{k=0}^(n)b^k = b^0 + b^1 + b^2 + ... + b^n` Deriving a closed form to this sum, we get: `\sum_{k=0}^(n)b^k = (b^(n+1) - 1) / (b-1)` For example, when `b=3` and `n=4`, we have: `3^0 + 3^1 + 3^2 + 3^3 + 3^4 = (3^(4+1) - 1) / (3-1)` All good so far. However, if we set `b=1`, we have a special case: `(1^(n+1) - 1) / (1-1) = 0/0` We know that `1^k=1` for any `k>=0`, therefore: `\sum_{k=0}^(n)1^k = n+1` but when `b=1`, our closed-form evaluates to `0/0` for any value of `n`. From this we can conclude that `0/0` does not have a certain value. Taking this example a little

Math is really fun, especially when is done symbolically. # Overview This time we're taking a look at some interesting relations and identities for fractions, which will give us an insight of what is really going on, for example, in an infinite sum and how we can analyze it by evaluating it symbolically. There is an useful and interesting identity for summing two fractions: $$\frac{a}{b} + \frac{c}{d} = \frac{ad + cb}{bd}$$ The question is: can we extend it to three fractions? What about ten? What about an infinite number of them? Well, yes, this is possible, and it's actually quite easy to find a general formula to this. To give you a taste how this can be analyzed, let's sum four fractions (using `a` for the numerator and `b` for the denominator, just for illustration, but they can have different values): $$\frac{a}{b} + \frac{a}{b} + \frac{a}{b} + \frac{a}{b} = \frac{b(b(b(a) + ab) + abb) + abbb}{bbbb}$$ Do you see the pattern? There is a b

Edge detection  is a fundamental tool in image processing, machine vision and computer vision. In this post we're going to take a look at a very basic edge detection algorithm, which takes into account a predefined tolerance value that can be adjusted to detect arbitrary fine details in a given image. # Algorithm The algorithm is extremely simple; it begins by iterating over each pixel in the image, then, for each pixel, it checks its neighbors. +-------+-------+-------+ |       |       |       | |   A   |   B   |   C   | |       |       |       | +-------+-------+-------+ |       |         |       | |   D   |         |   E   | |       |         |       | +-------+-------+-------+ |       |       |       | |   F   |   G   |   H   | |       |       |       | +-------+-------+-------+ If any two opposite neighbors differ in intensity by more than a predefined tolerance, then it marks the current pixel as part of an edge. The comparison is done by taking th

The Julia set and its complex beauty. A complex system in the Julia set can be defined as simply as: `z = z^2 + c` where both `z` and `c` are complex numbers. # Algorithm The value of `z` is updated iteratively for a predefined number of times (e.g.: 100) or while the absolute value of `z` is lower than a given constant (e.g. `\abs(z) < 2`). The initial value of `z` is set as: z = Complex ( ( 2 * x - w ) / ( w * zoom ) + moveX , ( 2 * y - h ) / ( h * zoom ) + moveY ) where `x` and `y` are the coordinate positions on a 2D plane, `w` and `h` are the width and height of the plane.  The values for "zoom", "moveX" and "moveY" are optional. They control the level of zoom into the fractal and the offsets for shifting the image on the X and Y axis. The iteration loop can be defined as: i = 100 # maximum number of iterations while ( abs ( z ) < 2 && -- i > 0

Infinity and its infinite beauty. Today we're going to take a brief look at the beauty of infinity, through: infinite sums infinite products continued fractions nested radicals and limits to represent some of the most well known and beautiful mathematical constants, like  π , e and φ . # Definitions Before diving into it, let's begin with some simple definitions: 1) Infinite sum: `\sum_{n=1}^(\infty)\frac{1}{n} = \frac{1}{1} + \frac{1}{2} + \frac{1}{3} + \...` 2) Infinite product: `\prod_{n=1}^(\infty)\frac{1}{n} = \frac{1}{1} * \frac{1}{2} * \frac{1}{3} * \...` 3) Continued fractions: `\underset{n=1}{\overset{\infty}{\mathbf{K}}}\frac{1}{n} = \frac{1}{1 + \frac{1}{2 + \frac{1}{3 + \...}}}` 4) Nested radicals: `\underset{n=1}{\overset{\infty}{\mathbf{R}}}(n + R)^(1/2) = \sqrt{1 + \sqrt{2 + \sqrt{3 + \...}}}` 5) Limit: `\lim_{n to \infty}(1 + 1/n)^n = (1 + 1/n)^n`, where `n` approaches `\infty`. # Infinite sums `\sum_{n=0}^(\in

In mathematics, a set is a collection of distinct objects, while a multiset  (or bag) is a generalization of the concept of a set, allowing multiple instances of a given object to exist in the same multiset. Working with multisets is a little bit more trickier and more computationally challenging, but it's quite fun, as we'll see in a moment. In programming, we can simulate a multiset using an array. The fun part comes when we have to implement some operations on this multisets, but we have to chose the right algorithms that will scale nicely and work efficiently even with multisets that contain more than a thousand elements. Before implementing the algorithms, let's take a brief look at some definitions of multiset operations. # Operations 1) Intersection (AND): The intersection of two multisets, A and B, denoted by A ∩ B, is the multiset of all things that are members of both A and B. [ 1 , 2 ] ∩ [ 2 , 3 ] = [ 2 ] [ 1 , 1 , 1 ,