Semiprime equationization
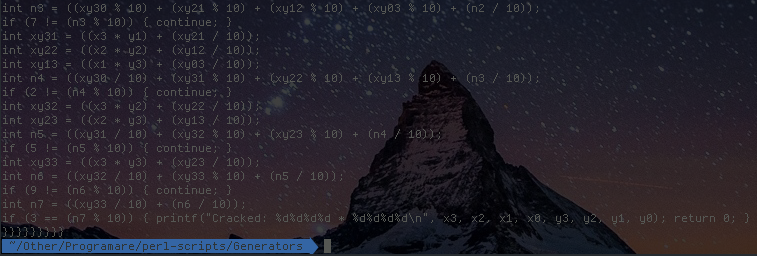
Prime numbers play an important role in cryptography due to the fact that it's hard to factorize a semiprime into its original two factors. A while ago, RSA put prizes on large semiprimes and challenged the public to crack them. Not surprisingly, most of the numbers remained unfactored until this day. The entire security system is based on the fact that we don't have a truly efficient factorization algorithm. To give you an example, using the most efficient known algorithm ( GNFS ), it took 5 months to factorize the RSA-640 number using 80 AMD Opteron CPUs, clocked at 2.2 GHz. But there is something special about the RSA semiprimes; all of them are the product of two prime numbers which have about the same length, with a deviation of ± 1 in some cases. This is a very valuable piece of information, because we can test only a restricted amount of prime numbers that are in the range we are interested in. For example, RSA-100 is a 100-digit number and is the product o